对数和分贝的话题
撰写于:2013年7月24日
作者:silex Wi-Fi专家
我们从事无线电工作的人经常使用“分贝(dB)”这个单位。“RSSI - 60db”、“最大输出14db”、“杂波智能5db”、“天线增益3db”等等。但是分贝到底是什么呢?这次就对数和分贝的话题,稍微夹杂着数学游戏进行介绍。
分贝和对数
维基百科上对分贝的定义是“用某物理量与基准量之比的常用对数表示”。也就是说,dB表示的是“比率”,即相对值,不是绝对值。
对数是乘数的反义词。10的3次方(10^3)是1000,而要把1000用常用对数表示的话就是log10(1000)=3。也就是说,对于L=logN(X), N^L=X是成立的,N则被称为“底”。“常用对数”是以10为底的对数(注),简单来说就是表示“有几个零”。log10(1000)=3,就是说明有3个零。如果是负值,这就是小数点,例如log10(0.001)=-3。对数不一定是整数,例如log10(20)可以是1.30103…的实数。
(※注)工学者使用以10为底的常用对数,而数学学者使用的是e=2.71828..为底的“自然对数”。有时用log()来表示常用对数,用ln()来表示自然对数。
以10为底的常用对数比被称为“贝尔(B)”单位,但贝尔这个单位很少被使用。技术人员常用的分贝(dB)是铃声的1/10,即10db = 1B。按道理来说,毫米贝尔(mB)和千兆(kB)这样的单位也是有可能的,但是除了分贝以外的对数表达几乎不被使用。0db等于10^0 = 1倍,1db等于10^0.1≈1.259倍,3db等于10^0.3≈1.995倍,10db等于10^1 = 10倍……就是这样的情况。
对数的好处在于可以用很小的数值来表现非常大范围的值。100万倍是log10(100万)= 60db(10的6次方),100兆倍是log10(100兆)= 140db(10的14次方)。龙珠的战斗力和肌肉男的友情力量也用dB来表现的话,就不需要那么多的零了。
另一个好处是可以用加法和减法替换乘法和除法。例如,100万×100兆就是log10(100万×100兆)= log10(100万)+ log10(100兆),那么马上就能得出200db(10的20次方)这样的值。因为传输系统中的增益和损失不是加法,而是乘法,所以用dB来计算就会变得简单一些。
对数和单位标记
dB是“比率”。因此,当我们说“对原来的产品改善了+ 3db”时,我们会知道“啊,相对来说是2倍啊(10^0.3=1.9952623)”,但“输出14db”或“天线增益3db”的基准是什么还不知道?实际上,这些数值都是以“dBm”或“dBi”为单位,dBm表示以1mW为基准的功率比,dBi表示以全方位无定向天线为基准的最大增益比。例如14dbm是1mW x 10^1.4,也就是大约25mW。dB、dBi和dBm应该被严格地区分使用,但它们常常被草率地写成“dB”。
为什么要特意用dB(dBm, dBi)来表示发射功率和天线增益呢?因为如上所述,传输系统的计算会变得轻松。发射功率14dbm,接收灵敏度- 60dbm,收发天线增益为6dbi,天线电缆损耗为- 3db,则功率差为14 - (-60)+ 6 -3= 77db,我们称之为Link Budget。由于伴随空间传输的电波衰减可以根据之前介绍过的弗里斯公式推算,例如2.4GHz,传输系数3.0,距离10m,损失约为70db,余量+ 7db,可以连续的计算。如果将距离增加到20m,损失则是79db,因此约有2db的不足,那么需要采取提高发射输出功率或提高接收灵敏度,或者提高天线增益以减少电缆损失等措施。如果将单位统一为dB的话,就可以用加法和减法来进行这样的计算了。
让我们用对数玩一玩
以X为底的对数来表示数值Y的n=logX(Y),表示用X进制来表示数值Y的时候是n位。掌握了这个基本原则,就能在很多方面发挥作用。
因为log的性质是logX(Y^Z) = Z * logX(Y),也就是说Y进制Z位数的数值用X进制来表示的话就是Z * logX(Y)位,意味着可以用位数来表达。例如,256比特可以表示的最大值是多少,不用一一计算2^256,256 * log10(2) = 256 * 0.30103 =十进制78,这样就知道是位数了。相反,在动画电影《夏日大作战》中,“使用2400位数素数的高级密码系统……”这是多少比特的密钥,2400 / 0.30103 = 7972.6273,所以“总之是8192bit的RSA密钥”。
还有一个对数的应用。我们在表示数字的时候用“进制”来表示,例如“95”这个数字是用十进制来表示的,二进制是“1011111”,十六进制是“5F”。进制越大位数越小,但每一位所需要的文字种类就越多。考虑一下转盘式的表盘显示,就很容易理解了吧。2进制的表盘显示,1位有2种显示方式就足够了,但相对的,数字会变多;10进制的表盘显示,数字会变少,但需要1位有10种文字的转盘。
那么,进制表记是大的好呢,还是小的好呢?或者哪里是最合适的呢?这个也可以用对数求出来。
X进制的数值是“X种符号以Z位排列”,因此其信息量为X*Z。任意的数Y用X进制表示的位数是Z=logX(Y),所以Y用X进制表示的信息量是X logX(Y)。对于进制数X,信息量在哪里最小,用X来微分就可以知道。
有任意底X的logX(Y)可以用自然对数转换成log(Y)/log(X),所以信息量是X logX(Y) = log(Y)/log(X)。这里的log(Y)是对任意的数Y确定的常数,所以变动成分(假设称为信息量系数)是X/log(X)。如果我们用X对它进行微分,那么根据商微分定律可获得:
f(x)/g(x) (f'(x)?g(x) - f(x)?g'(x))/{g(x)}^2
f(x) = X
g(x) = log(X)
f'(x) = 1
g'(x) = 1/X
所以
(f'(x)?g(x) - f(x)?g'(x))/{g(x)}^2 = (log(X) - X*1/X) / (log(X)^2)
= (log(X) - 1) / log(X)^2
= log(X) - 1/log(X)^2
这个微分函数f’(x)的零点是f(x)的最低点,它是log(x) =1的点,即x =e (e=自然对数的底,e=2.71828…)的情况。但现实问题是,由于进制是整数,所以与2.7最接近的整数三进制是信息效率最高的进制方式。
信息量系数 X/log(X) 实际标注如下图所示。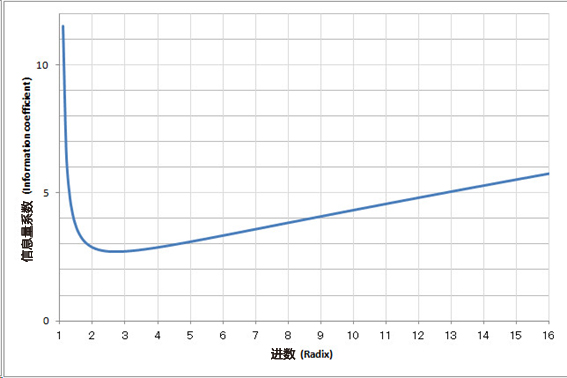
进制数低于2时信息量会急剧发散,而超过2则达到2.7的最低点,之后会微幅增加。对于进制x的系数:
x=2.0 2.885
x=2.7 2.718
x=3.0 2.731
x=4.0 2.885
x=10.0 4.343
x=12.0 4.829
x=16.0 5.794
因此,即使说三进制比二进制效率好,其差距也只有5.4%。另一方面,与二进制相比,十进制需要1.5倍的信息量,十六进制需要2倍的信息量。现在的计算机基本上是用二进制来处理信息的,除了“可以按ON/OFF进行设计,电路变得简单”以外,还有这样的数学原理。
说起来,我还记得很久以前,某大型电器制造商为了宣传“开发出了四值逻辑的计算机”,把二值单色图像和四值灰色图像用在报纸上来宣传。就连当时还是高中生的我都认为“像素亮度深度和逻辑运算单位是不一样的吧”,但是在上述的估算中,2值和4值的信息效率是一样的,所以会认为电路越复杂,4值就越不利。现在想来那应该是与产品价值无关的研究所的成果发表和股价对策。光计算机和第五代计算机(笑)被称为“下一代”计算机,很多大型日本企业都将丰厚的资金投资于这些下一代技术的研究,真是老套啊。这是时代的故事。
嵌入式无线LAN模块产品介绍页面
分贝和对数
维基百科上对分贝的定义是“用某物理量与基准量之比的常用对数表示”。也就是说,dB表示的是“比率”,即相对值,不是绝对值。
对数是乘数的反义词。10的3次方(10^3)是1000,而要把1000用常用对数表示的话就是log10(1000)=3。也就是说,对于L=logN(X), N^L=X是成立的,N则被称为“底”。“常用对数”是以10为底的对数(注),简单来说就是表示“有几个零”。log10(1000)=3,就是说明有3个零。如果是负值,这就是小数点,例如log10(0.001)=-3。对数不一定是整数,例如log10(20)可以是1.30103…的实数。
(※注)工学者使用以10为底的常用对数,而数学学者使用的是e=2.71828..为底的“自然对数”。有时用log()来表示常用对数,用ln()来表示自然对数。
以10为底的常用对数比被称为“贝尔(B)”单位,但贝尔这个单位很少被使用。技术人员常用的分贝(dB)是铃声的1/10,即10db = 1B。按道理来说,毫米贝尔(mB)和千兆(kB)这样的单位也是有可能的,但是除了分贝以外的对数表达几乎不被使用。0db等于10^0 = 1倍,1db等于10^0.1≈1.259倍,3db等于10^0.3≈1.995倍,10db等于10^1 = 10倍……就是这样的情况。
对数的好处在于可以用很小的数值来表现非常大范围的值。100万倍是log10(100万)= 60db(10的6次方),100兆倍是log10(100兆)= 140db(10的14次方)。龙珠的战斗力和肌肉男的友情力量也用dB来表现的话,就不需要那么多的零了。
另一个好处是可以用加法和减法替换乘法和除法。例如,100万×100兆就是log10(100万×100兆)= log10(100万)+ log10(100兆),那么马上就能得出200db(10的20次方)这样的值。因为传输系统中的增益和损失不是加法,而是乘法,所以用dB来计算就会变得简单一些。
对数和单位标记
dB是“比率”。因此,当我们说“对原来的产品改善了+ 3db”时,我们会知道“啊,相对来说是2倍啊(10^0.3=1.9952623)”,但“输出14db”或“天线增益3db”的基准是什么还不知道?实际上,这些数值都是以“dBm”或“dBi”为单位,dBm表示以1mW为基准的功率比,dBi表示以全方位无定向天线为基准的最大增益比。例如14dbm是1mW x 10^1.4,也就是大约25mW。dB、dBi和dBm应该被严格地区分使用,但它们常常被草率地写成“dB”。
为什么要特意用dB(dBm, dBi)来表示发射功率和天线增益呢?因为如上所述,传输系统的计算会变得轻松。发射功率14dbm,接收灵敏度- 60dbm,收发天线增益为6dbi,天线电缆损耗为- 3db,则功率差为14 - (-60)+ 6 -3= 77db,我们称之为Link Budget。由于伴随空间传输的电波衰减可以根据之前介绍过的弗里斯公式推算,例如2.4GHz,传输系数3.0,距离10m,损失约为70db,余量+ 7db,可以连续的计算。如果将距离增加到20m,损失则是79db,因此约有2db的不足,那么需要采取提高发射输出功率或提高接收灵敏度,或者提高天线增益以减少电缆损失等措施。如果将单位统一为dB的话,就可以用加法和减法来进行这样的计算了。
让我们用对数玩一玩
以X为底的对数来表示数值Y的n=logX(Y),表示用X进制来表示数值Y的时候是n位。掌握了这个基本原则,就能在很多方面发挥作用。
因为log的性质是logX(Y^Z) = Z * logX(Y),也就是说Y进制Z位数的数值用X进制来表示的话就是Z * logX(Y)位,意味着可以用位数来表达。例如,256比特可以表示的最大值是多少,不用一一计算2^256,256 * log10(2) = 256 * 0.30103 =十进制78,这样就知道是位数了。相反,在动画电影《夏日大作战》中,“使用2400位数素数的高级密码系统……”这是多少比特的密钥,2400 / 0.30103 = 7972.6273,所以“总之是8192bit的RSA密钥”。
还有一个对数的应用。我们在表示数字的时候用“进制”来表示,例如“95”这个数字是用十进制来表示的,二进制是“1011111”,十六进制是“5F”。进制越大位数越小,但每一位所需要的文字种类就越多。考虑一下转盘式的表盘显示,就很容易理解了吧。2进制的表盘显示,1位有2种显示方式就足够了,但相对的,数字会变多;10进制的表盘显示,数字会变少,但需要1位有10种文字的转盘。
那么,进制表记是大的好呢,还是小的好呢?或者哪里是最合适的呢?这个也可以用对数求出来。
X进制的数值是“X种符号以Z位排列”,因此其信息量为X*Z。任意的数Y用X进制表示的位数是Z=logX(Y),所以Y用X进制表示的信息量是X logX(Y)。对于进制数X,信息量在哪里最小,用X来微分就可以知道。
有任意底X的logX(Y)可以用自然对数转换成log(Y)/log(X),所以信息量是X logX(Y) = log(Y)/log(X)。这里的log(Y)是对任意的数Y确定的常数,所以变动成分(假设称为信息量系数)是X/log(X)。如果我们用X对它进行微分,那么根据商微分定律可获得:
f(x)/g(x) (f'(x)?g(x) - f(x)?g'(x))/{g(x)}^2
f(x) = X
g(x) = log(X)
f'(x) = 1
g'(x) = 1/X
所以
(f'(x)?g(x) - f(x)?g'(x))/{g(x)}^2 = (log(X) - X*1/X) / (log(X)^2)
= (log(X) - 1) / log(X)^2
= log(X) - 1/log(X)^2
这个微分函数f’(x)的零点是f(x)的最低点,它是log(x) =1的点,即x =e (e=自然对数的底,e=2.71828…)的情况。但现实问题是,由于进制是整数,所以与2.7最接近的整数三进制是信息效率最高的进制方式。
信息量系数 X/log(X) 实际标注如下图所示。

进数和信息量系数(显示)
进制数低于2时信息量会急剧发散,而超过2则达到2.7的最低点,之后会微幅增加。对于进制x的系数:
x=2.0 2.885
x=2.7 2.718
x=3.0 2.731
x=4.0 2.885
x=10.0 4.343
x=12.0 4.829
x=16.0 5.794
因此,即使说三进制比二进制效率好,其差距也只有5.4%。另一方面,与二进制相比,十进制需要1.5倍的信息量,十六进制需要2倍的信息量。现在的计算机基本上是用二进制来处理信息的,除了“可以按ON/OFF进行设计,电路变得简单”以外,还有这样的数学原理。
说起来,我还记得很久以前,某大型电器制造商为了宣传“开发出了四值逻辑的计算机”,把二值单色图像和四值灰色图像用在报纸上来宣传。就连当时还是高中生的我都认为“像素亮度深度和逻辑运算单位是不一样的吧”,但是在上述的估算中,2值和4值的信息效率是一样的,所以会认为电路越复杂,4值就越不利。现在想来那应该是与产品价值无关的研究所的成果发表和股价对策。光计算机和第五代计算机(笑)被称为“下一代”计算机,很多大型日本企业都将丰厚的资金投资于这些下一代技术的研究,真是老套啊。这是时代的故事。
嵌入式无线LAN模块产品介绍页面






